【機械学習】特徴量とは？意味や変数、選択について

特徴量とは

特徴量（feature）とはモデルが予測を行うために使うことができるデータの特性または属性のことです。よりわかりやすく言うと、
特徴量はデータの中から予測・分類するための手掛かりとなる変数です。

機械学習は大量のデータを学習し、未知のデータを分類または将来を予測することを目的としています。この目的を果たすためにデータの特徴（特徴量）に着目し、目的を達成できる学習済みモデルを構築します。

イメージしやすいのが、データがテーブル（表形式）に含まれている場合は、テーブルの列が特徴量となります。

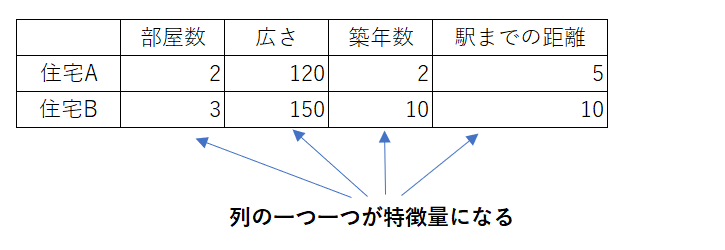
特徴量の例を挙げると、例えばスパムメールを判別するモデルでは、メールに含まれる単語や送信者、メールサイズなどが特徴量となります。または住宅価格の予測では、部屋の数や広さ、築年数、駅までの距離、地域の犯罪率などが特徴量です。
上記からわかるように、データを説明するものが特徴量と言えます。

特徴量は数値（特徴抽出）

ご存じのようにコンピューターはあくまでも計算機であるため、学習で扱えるものは数値のみです。そのため特徴量は数値で表す必要があります。

機械学習を用いた製品に、人間の言葉を理解するものや画像を判別するものがあります。音声や画像のような数値化されていないデータをそのまま用いることはできないため、製品内部ではコンピューターが扱える数値に変換して動いています。

このようなデータを特徴量に変換する作業を特徴抽出と呼びます。

特徴量の質

機械学習で最終的に求められるのは精度の高い予測・分類です。精度の高いモデルを作成するためには質の良い特徴量が不可欠になります。

特徴量の質は選択する特徴量によっても変わりますし、前処理によるデータ形式の変換にもよります。

機械学習における前処理については以下記事をご参照ください。

【機械学習】データの前処理：データ操作について

特徴量の質が悪いと、その分機械学習による予測・分類の精度が低くなるため、機械学習において「データの前処理」は重要な役割を果たしています。

目的変数

求めたいもの（予測・分類したいもの）の過去データを目的変数と呼びます。

例では、求めたい「住宅価格」の過去データである「住宅価格」が目的変数となります。

説明変数

目的変数に影響を与える（原因となっている）ものを説明変数と呼びます。そして説明変数は特徴量とイコールの関係です。

例では、目的変数（住宅価格）に影響を与える「部屋数」、「広さ」、「築年数」、「駅までの距離」が説明変数となります。

フィルタ法

フィルタ法とは各特徴を統計的に点数化し、その点数から特徴量を選び出す手法です。フィルタ法は単変量特徴量選択とも呼ばれます。

特徴量を点数化する手法としては、「カイ二乗検定（Chi-Square）」や「ANOVA（Analytics of Variance）」などが存在します。

組み込み法

組み込み法とは機械学習モデルが学習中に特徴量選択を行う手法です。組み込み法はモデルベース特徴量選択とも呼ばれます。

学習アルゴリズムに特徴量選択が組み込まれていることから、組み込み法と呼ばれています。

簡単に言うと、組み込み法は学習と特徴量選択を同時に行うということです。

組み込み法のアルゴリズムには、「決定木」や「ラッソ回帰」などがあります。

ラッパー法

ラッパー法（Wrapper Method）とは複数の特徴を組み合わせて、最も精度が高い組み合わせを探索する手法です。ラッパー法は反復特徴量選択とも呼ばれます。

様々な特徴量の組み合わせを試すため、特徴量が多いと膨大な計算が必要となります。